Welcome to xpt’s blog! 2021年准备秋招期间整理的一些笔记，分享给大家！

文档分享的初衷是给师弟师妹们作为参考，主要是适合想去大厂+测试开发岗的朋友们。
建议大家自己整理文档，把我的文档作为参考，有些东西自己整理，自己去写出来，才是最适合你自己的！
文章还未精细整理，如存在错误之处，可以邮件or微信反馈给我呀，感激不尽！

想进大厂，要抓住提前批免笔试的机会！（例如京东、字节、百度等报名时间一般为七月，面试时间为报名后的一周内，面试一般为3轮，面试相关经验后续我会单独再写blog分享^_^，也欢迎大家来跟我talk，一定知无不言。）

本人情况：普通211、研究生、有京东、百度、以及字节提前批测开岗offer。7月初开始准备，准备太迟，一边准备一边投简历+面试。

投递简历时间：京东（7.14），字节（7.30），百度（7.30）
三轮面试时间：京东（7.21-7.22-7.26），字节（8.4-8.6-8.9），百度（8.9-8.12-8.16）
意向书时间：京东（8.12），字节（8.16），百度（9.9）

京东提前批开始很早，我投的时候已经是第二批。经过京东几轮面试，熟悉了面试流程，大概掌握了测开岗会问些什么问题。
字节和百度提前批我是在ddl前一天投递，其实已经算很迟了，hc不多了。
投递要趁早，很多岗位有固定hc。
多拿offer，才有谈薪资的底气。

我面试的岗位有以下：
1、测试开发岗（京东、百度、以及字节提前批）
2、银行java开发岗（所以我会整理一点java，银行问的都很简单，所以我这里对java的整理比较少）

整理的内容均来源于历年网络上分享的面经（主要来源于牛客），以及我面试时被问过的问题，list如下：
(1)——计算机网络
(2)——操作系统
(3)——数据库
(4)——数据结构
(5)——python
(6)——java
(7)——linux
(8)——常考编程题
(9)——测试开发相关知识

面试QA整理(4)——数据结构

数组和链表的区别，优缺点

数组的特点：元素增删慢，查找快

数组将元素在内存中连续存放，由于每个元素占用内存相同，可以通过下标迅速访问数组中任何元素。
数组的插入数据和删除数据效率低，插入数据时，这个位置后面的数据在内存中都要向后移。删除数据时，这个数据后面的数据都要往前移动。
数组的随机读取效率很高。因为数组是连续的，知道每一个数据的内存地址，可以直接找到相应数据。
如果应用需要快速访问数据，很少或不插入和删除元素，就应该用数组。
数组需要预留空间，在使用前要先申请占内存的大小，可能会浪费内存空间。
并且数组不利于扩展，数组定义的空间不够时要重新定义数组。

链表的特点： 元素增删快，查找慢

链表中的元素在内存中不是顺序存储的，而是通过存在元素中的指针联系到一起。
如果要访问链表中一个元素，需要从第一个元素开始，一直找到需要的元素位置。
增加和删除一个元素对于链表数据结构非常简单，只要修改元素中的指针就可以了。
如果应用需要经常插入和删除元素你就需要用链表数据结构了。
不指定大小，扩展方便。链表大小不用定义，数据随意增删。

数组的优点：

随机访问性强
查找速度快

数组的缺点:

插入和删除效率低
可能浪费内存
内存空间要求高，必须有足够的连续内存空间。
数组大小固定，不能动态拓展

链表的优点:

插入删除速度快
内存利用率高，不会浪费内存
大小没有固定，拓展很灵活。

链表的缺点：不能随机查找，必须从第一个开始遍历，查找效率低

队列和栈有什么区别

队列是在队尾入队，队头出队，即两边都可操作。

而栈的进栈和出栈都是在栈顶进行的，无法对栈底直接进行操作。

队列是先进先出（FIFO），即队列的修改是依先进先出的原则进行的。新来的成员总是加入队尾（不能从中间插入），每次离开的成员总是队列头上（不允许中途离队）。

而栈为先进后出,即每次删除（出栈）的总是当前栈中最新的元素，即最后插入（进栈）的元素，而最先插入的被放在栈的底部，要到最后才能删除。

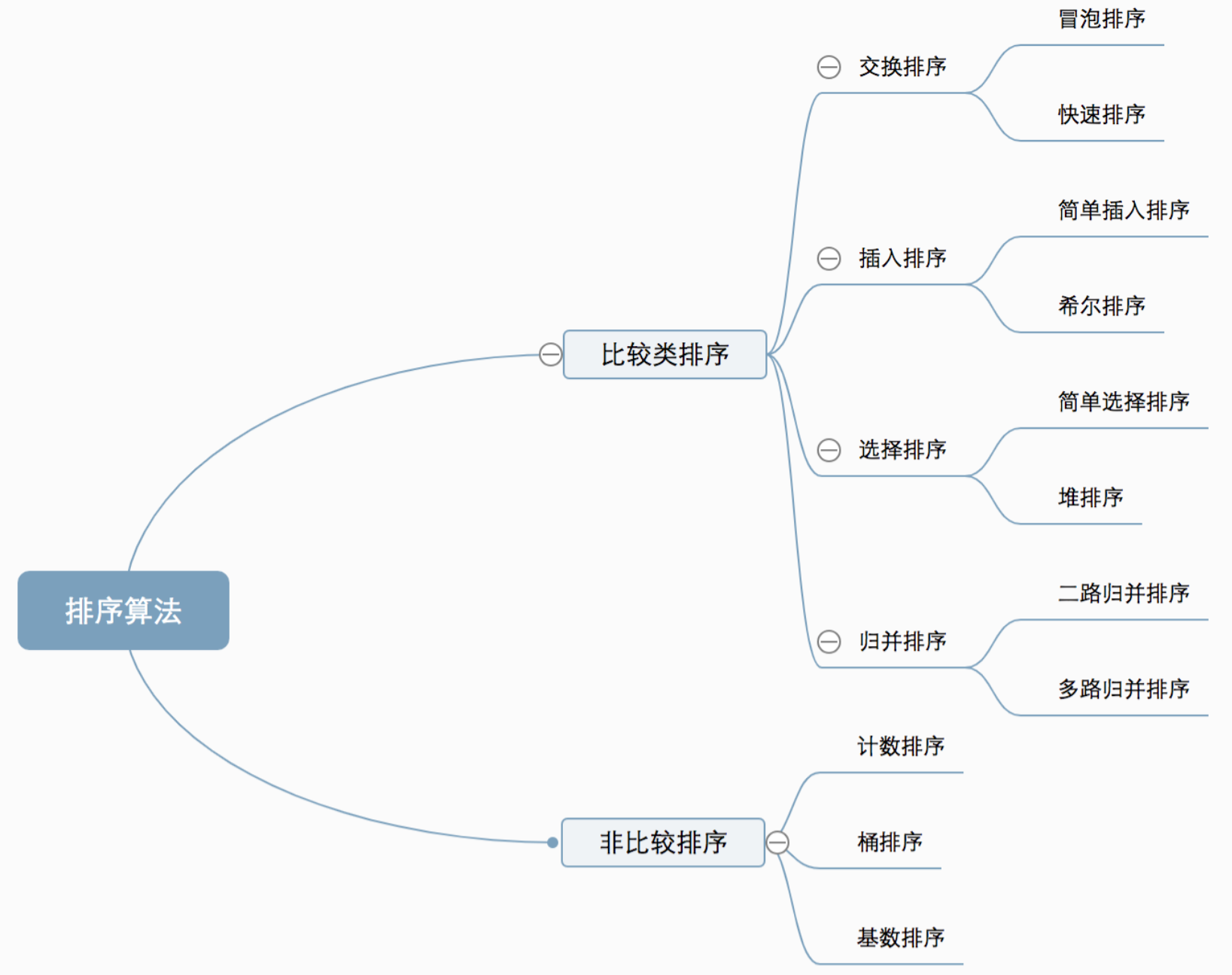
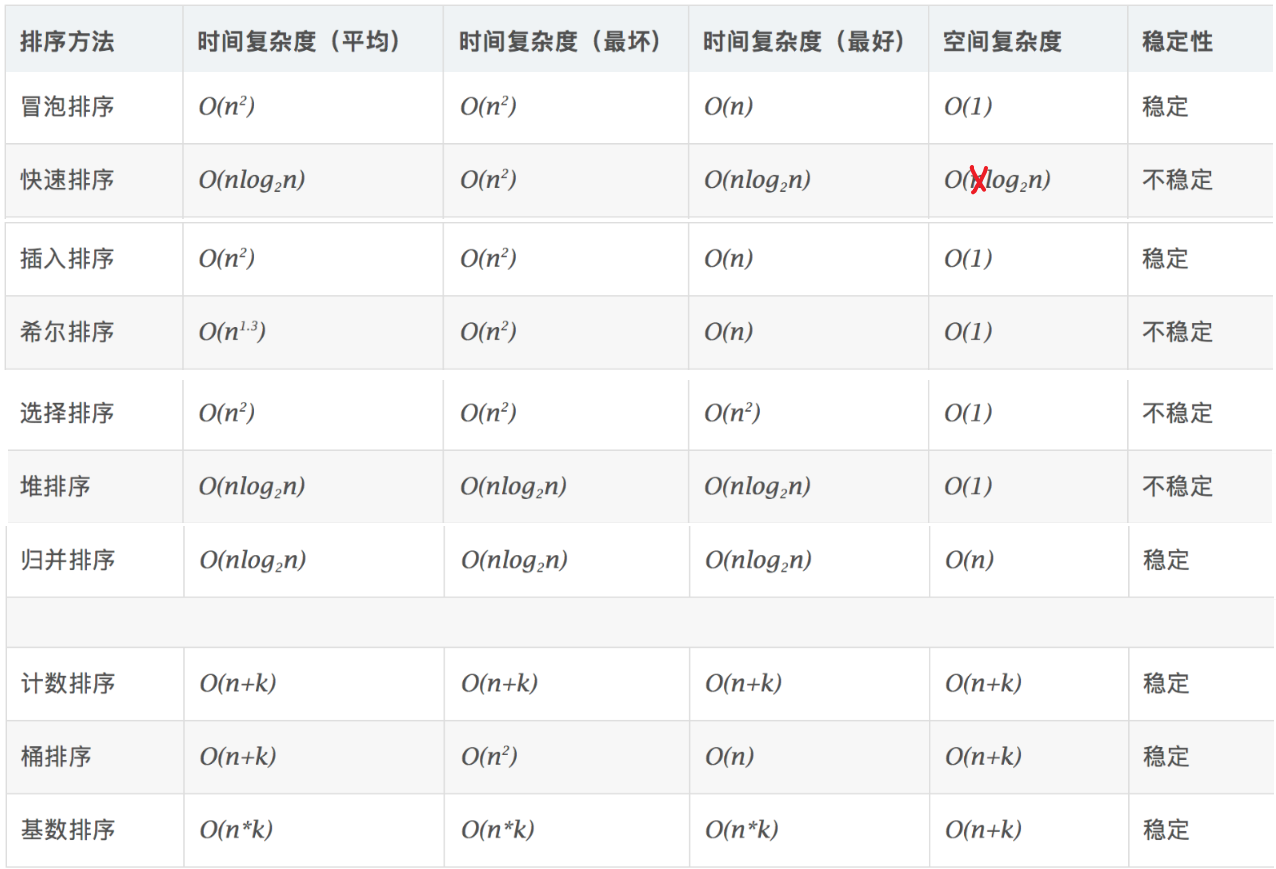
二分法的原理阐述，时间复杂度与空间复杂度

排序算法（复杂度

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

冒泡排序(Bubble Sort)

冒泡排序(Bubble Sort)一种交换排序，它的基本思想是:两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

冒泡排序对n个数据操作n-1轮，每轮找出一个最大（小）值。

**最好时间复杂度：O(n)**。当输入数组刚好是顺序的时候，只需要挨个比较一遍就行了，不需要做交换操作。

**最坏时间复杂度：O(n^2)**。当数组刚好是完全逆序的时候，每轮排序都需要挨个比较 n 次，并且重复 n 次。

**平均时间复杂度：O(n^2)**。当输入数组杂乱无章时，每轮排序都需要挨个比较 n 次，并且重复 n 次。

**空间复杂度：O(1)**。使用了交换法，不需要开辟额外的空间。

稳定性：元素相同时不做交换，是稳定的排序算法。

def BubbleSort(array):
    lens = len(array)
    if (lens<2):
        return array
    for i in range(lens-1): #注意range左闭右开 只需要排前n-1个数，排好了，最后一个数也就排好了
        for j in range(lens-1-i):
            if array[j]>array[j+1]:
                array[j+1],array[j]=array[j],array[j+1]
    return array


if __name__ == '__main__':
    array_test = [12, 23, 54, 32, 11, 5, 73]
    print(BubbleSort(array_test)) #[5, 11, 12, 23, 32, 54, 73]

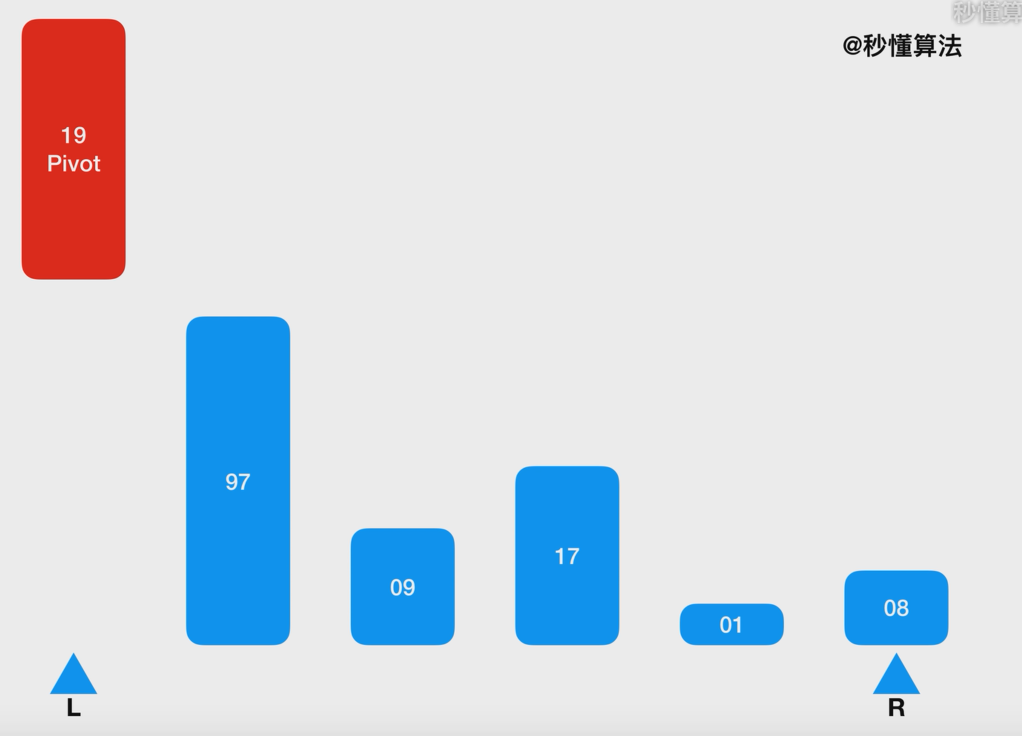
快速排序(Quick Sort)

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

从数列中挑出一个元素，称为 “基准”（pivot）；
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

**最好时间复杂度：O(nlogn)**。每次选取分区点时，都能选中中位数，把数组等分成两个。

【基准值若能把数据分为平均的两块，划分次数O(logn)，每次划分遍历比较一遍O(n)，时间复杂度O(nlogn)。】

最坏时间复杂度：O(n^2)。每次分区都选中了最小值或最大值，得到不均等的两组。那么就需要 n 次的分区操作。

平均时间复杂度：O(nlogn)。在大部分情况下，统计上是很难选到极端情况的，因为大多数时候都不是选中最大或最小值。

空间复杂度：额外空间开销出在暂存基准值，O(logn)次划分需要O(logn)个，**空间复杂度O(logn)**。

稳定性：快速排序的分区过程涉及交换操作，是不稳定的排序算法。

def Partion(array, l, r):
    pivot = array[l]
    while (l < r):
        while (l < r and array[r] >= pivot):
            r -= 1
        array[l] = array[r]
        while (l < r and array[l] <= pivot):
            l += 1
        array[r] = array[l]

    array[l] = pivot
    return l
               
def QuickSort(array, l, r):
    if (l < r): #不能忘记！！！！！！！！！
        p = Partion(array, l, r)
        QuickSort(array, l, p - 1)
        QuickSort(array, p + 1, r)
        return array                

if __name__ == '__main__':
    array_test = [19, 97, 9, 17, 1, 8]
    print(QuickSort(array_test, 0, len(array_test) - 1))  # [1, 8, 9, 17, 19, 97]

简单插入排序(Insertion Sort）

插入排序（Insertion-Sort）是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

从第一个元素开始，该元素可以认为已经被排序；
取出下一个元素，在已经排序的元素序列中从后向前扫描；
如果该元素（已排序）大于新元素，将该元素移到下一位置；
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
将新元素插入到该位置后；
重复步骤2~5。

简单插入排序同样操作n-1轮，每轮将一个未排序数插入排好序列。

最好时间复杂度：O(n)。当数组刚好是完全顺序时，每次只用比较一次就能找到正确的位置；这个过程重复 n-1次，就可以清空未排序区间。

最坏时间复杂度：O(n^2)。当数组刚好是完全逆序时，要比较1+2+3+….+n-1 次才能找到正确位置；这个过程重复 n-1次，就可以清空未排序区间。

平均时间复杂度：O(n^2)。开始时默认第一个数有序，将剩余n-1个数逐个插入。插入操作具体包括：比较确定插入位置，数据移位腾出合适空位。每轮操作O(n)次，共O(n)轮，时间复杂度O(n^2)。

空间复杂度：O(1)。额外空间开销出在数据移位时那一个过渡空间，空间复杂度O(1)。

稳定性：元素相同时不做交换，是稳定的排序算法。

def InsertSort(array):
    lens = len(array)
    if lens < 2:
        return array
    for i in range(1, lens):
        target = array[i]  # 每次循环的一个待插入的数
        j = i - 1  # 从等待插入的前一个数开始比较，一直往左移动比较
        while j >= 0 and target < array[j]:
            array[j + 1] = array[j]  # 待插入的小，交换
            j -= 1
        array[j + 1] = target
    return array


if __name__ == '__main__':
    array_test = [19, 97, 9, 17, 1, 8]
    print(InsertSort(array_test)) #[1, 8, 9, 17, 19, 97]

希尔排序(Shell Sort)

1959年Shell发明，第一个突破O(n^2)的排序算法，是简单插入排序的改进版。

它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序。

若序列基本有序，简单插入排序不必做很多移动操作，效率很高。

希尔排序将序列按固定间隔划分为多个子序列，在子序列中简单插入排序，先做远距离移动使序列基本有序；逐渐缩小间隔重复操作，最后间隔为1时即简单插入排序。

def ShellSort(array):
    lens = len(array)
    if lens < 2:
        return array

    step = lens // 2  # 设定初始步长,注意整除
    while step > 0:
        for i in range(step, lens):
            # 类似插入排序, 当前值与指定步长之前的值比较, 符合条件则交换位置
            while i >= step and array[i] < array[i - step]:
                array[i], array[i - step] = array[i - step], array[i]
                i -= step
        step = step // 2
    return array


if __name__ == '__main__':
    array_test = [19, 97, 9, 17, 1, 8]
    print(ShellSort(array_test))  # [1, 8, 9, 17, 19, 97]

简单选择排序(Select Sort)

选择排序(Selection-sort)：简单选择排序同样对数据操作n-1轮，每轮找出一个最小（大）值。以此类推，直到所有元素均排序完毕。

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。

时间复杂度O(n^2)。

def SelectSort(array):
    lens = len(array)
    if lens < 2:
        return array

    for i in range(0, lens - 1):
        minIndex = i  # 将当前下标定义为最小值下标
        for j in range(i + 1, lens):  # 循环i后面的数据
            if (array[j] < array[minIndex]):  # 把数据小的下边赋给minIndex
                minIndex = j
        if (minIndex != i):  # 找到了一个最小值
            array[i], array[minIndex] = array[minIndex], array[i]
    return array


if __name__ == '__main__':
    array_test = [19, 97, 9, 17, 1, 8]
    print(SelectSort(array_test))  # [1, 8, 9, 17, 19, 97]

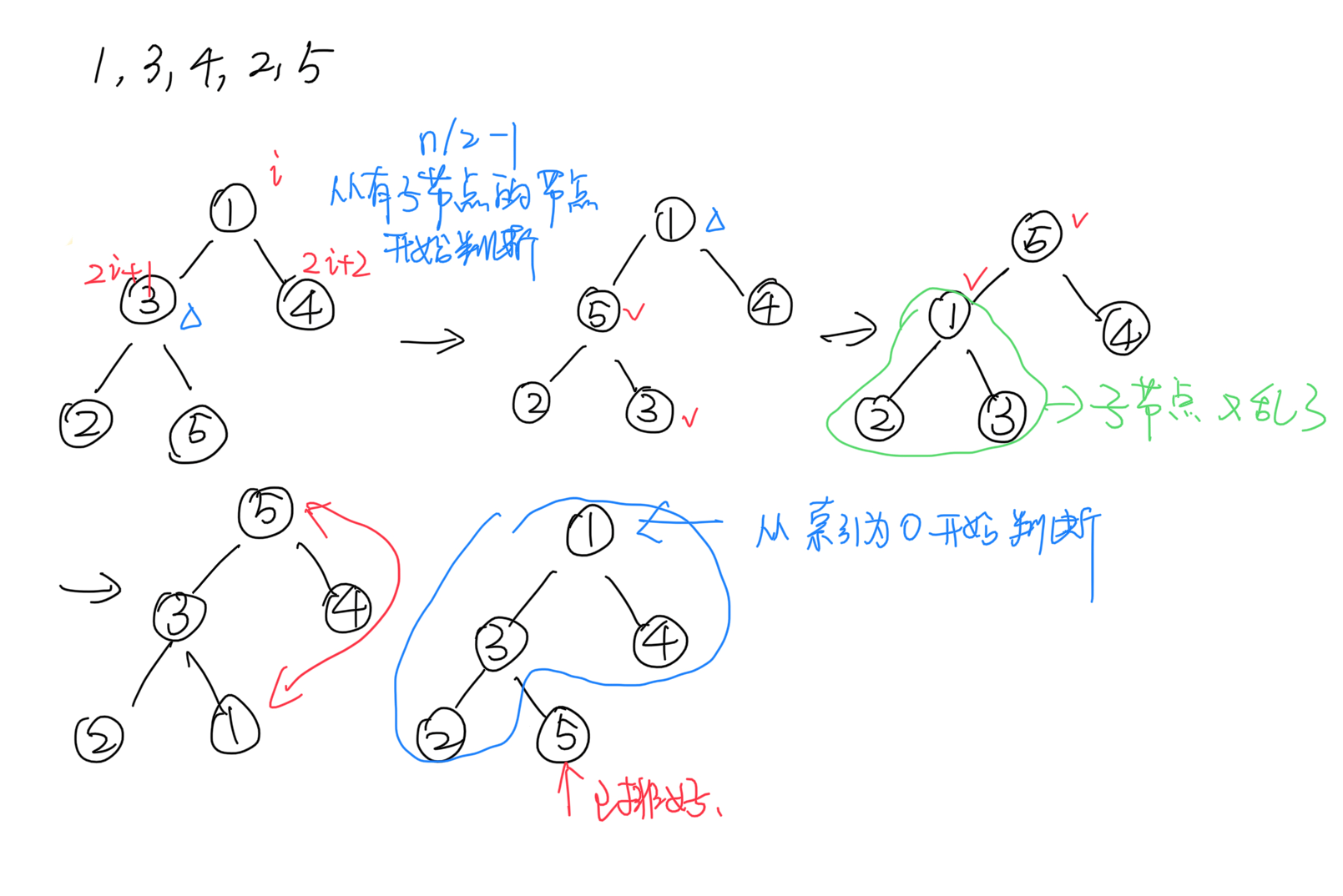
堆排序(Heap Sort)

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆排序过程

1.构造一个大顶堆，取堆顶数字R[1] (也就是最大值)与最后一个元素R[n]交换
2.新的无序区(R1,R2,……Rn-1)和新的有序区(Rn)。再将剩下的数字构建一个大顶堆，取堆顶数字(也就是剩下值当中的最大值)R[1]与无序区最后一个元素交换
3.得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。
4.重复以上操作，直到取完堆中的数字，最终得到一个从大到小排列的序列

堆排序的初始建堆过程比价复杂，对O(n)级别个非叶子节点进行堆调整操作O(logn)，时间复杂度O(nlogn)；

之后每一次堆调整操作确定一个数的次序，时间复杂度O(nlogn)。

合起来时间复杂度O(nlogn)

额外空间开销出在调整堆过程，根节点下移交换时一个暂存空间，空间复杂度O(1)

# 构建大顶堆
def HeadAdjust(array, i, n):  # 以i为根节点进行堆调整为大顶堆
    largest = i  # 创建一个索引，后面用于交换
    l = 2 * i + 1  # 左孩子
    r = 2 * i + 2  # 右孩子

    if l < n and array[i] < array[l]:  # 左孩子比根节点大
        largest = l
    if r < n and array[largest] < array[r]:  # 右孩子更大
        largest = r
    if largest != i:
        array[i], array[largest] = array[largest], array[i]
        HeadAdjust(array, largest, n)  # 堆顶排好了，但是子堆又混乱了，需要重新排

def HeapSort(array):
    n = len(array)

    # 构建第一个大顶堆
    for i in range(n // 2 - 1, -1, -1):  # 从有子节点的节点开始判断就行
        HeadAdjust(array, i, n)

    # 一个个交换元素
    for i in range(n - 1, 0, -1):  # 循环i从n-1开始;下一次创建堆i=n-2，不会带上已经排好的元素，排好n-1个，所以左闭右开，右不需要写-1，写0就行
        array[i], array[0] = array[0], array[i]  # 将堆顶元素和末尾元素做交换
        HeadAdjust(array, 0, i)  # 再构建新的大顶堆，从被换上去的那个数开始判断就行，也就是索引0处，因为除了它，其它已经构建好
    return array


if __name__ == '__main__':
    array_test = [1, 3, 4, 2, 5]
    print(HeapSort(array_test))  # [1, 2, 3, 4, 5]

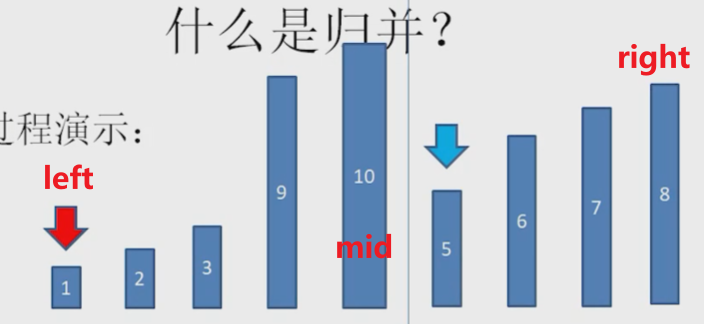
归并排序（Merge Sort）

归并排序的原理其实就是分治法。它首先将数组不断地二分，直到最后每个部分只包含 1 个数据。然后再对每个部分分别进行排序，最后将排序好的相邻的两部分合并在一起，这样整个数组就有序了。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

1.将序列中带排序数字分为若干组，每个数字分为一组
2.将若干个组两两合并，保证合并后的组是有序的
3.重复第二步操作直到只剩下一组，排序完成

把长度为n的输入序列分成两个长度为n/2的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。

性能

最好、最坏、平均时间复杂度：O(nlogn)。采用了二分的迭代方式，复杂度是 O(logn)。每次的迭代，需要对两个有序数组进行合并，这样的动作在 O(n) 的时间复杂度下就可以完成。同时，它的执行频次与输入序列无关。

空间复杂度：O(n)。每次合并的操作都需要开辟基于数组的临时内存空间。

稳定性：合并的时候，相同元素的前后顺序不变，是稳定的排序算法。

def Merge(array, left, mid, right):
    temp = []  # 临时数组
    i = left  # 左段子序列起始
    j = mid + 1  # 右段子序列起始
    while i <= mid and j <= right:
        if array[i] <= array[j]:
            temp.append(array[i])
            i += 1
        else:
            temp.append(array[j])
            j += 1
    # while循环结束后，有一部分会没有数了
    # 如果是左部分没数了
    while i <= mid:
        temp.append(array[i])
        i += 1
    # 如果是右部分没数了
    while j <= right:
        temp.append(array[j])
        j += 1
    # 把临时数组赋给原数组,注意下标
    array[left:right + 1] = temp


def MergeSort(array, left, right):
    if (left < right):  # 判断列表有至少有两个数字，如果left=right,说明只有一个元素，不用排序
        mid = (left + right) // 2
        MergeSort(array, left, mid)
        MergeSort(array, mid + 1, right)
        Merge(array, left, mid, right)
        return array


if __name__ == '__main__':
    array_test = [19, 97, 9, 17, 1, 8]
    print(MergeSort(array_test, 0, len(array_test) - 1))  # [1, 8, 9, 17, 19, 97]

二叉树的遍历

创建节点

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

递归（前序、中序、后序

# 先(前)序遍历：根——左——右
def PreOrder(root, array=[]):
    if root == None:
        return
    array.append(root.val)
    PreOrder(root.left, array)
    PreOrder(root.right, array)
    return array

# 中序遍历：左——根——右
def InOrder(root, array=[]):
    if root == None:
        return
    InOrder(root.left, array)
    array.append(root.val)
    InOrder(root.right, array)
    return array

# 后序遍历：左——右——根
def PostOrder(root, array=[]):
    if root == None:
        return
    PostOrder(root.left, array)
    PostOrder(root.right, array)
    array.append(root.val)
    return array

非递归（前序、中序、后序

# 深度优先遍历DFS (非递归——前序：根，左，右)
# 思想：利用栈，先将根入栈，再将根出栈；并将根的右子树，左子树存入栈，按照栈的先进后出规则来实现深度优先遍历。
# 有右节点先压右节点，再压左节点
def DFS(root):
    if root == None:
        return
    stack = [root]  # 栈用来保存未访问节点
    array = []  # 保存节点值，作为结果

    while stack:
        s = stack.pop()  # 拿出栈顶节点
        array.append(s.val)
        if s.right:
            stack.append(s.right)  # 先存右子树
        if s.left:
            stack.append(s.left)
    return array


# 非递归——中序遍历：左——根——右
# 思想：按照栈的先进后出规则来实现
def InOrder2(root):
    if root == None:
        return
    stack = []  # 栈用来保存未访问节点
    array = []  # 保存节点值，作为结果
    while stack or root:
        while root:
            # 从根节点开始，一直找它的左子树
            # 依次压入栈中
            stack.append(root)
            root = root.left  # 一直往下找左子树
        # while结束表示当前节点root为空，即当前节点没有左子树了

        root = stack.pop()  # 从最左开始弹出
        array.append(root.val)
        # 如果当前根节点有右子树
        root = root.right
    return array


# 非递归——后序遍历：左——右——根
# 思想：按照栈的先进后出规则来实现
# (ye是根右左的逆序)

def PostOrder2(root):
    if root == None:
        return
    stack = []
    array = []

    while stack or root:
        while root:
            stack.append(root)
            if root.left:
                root = root.left
            else:
                root = root.right

        root = stack.pop()
        array.append(root.val)
        # 栈不空且刚刚弹出的是左子节点，那么应当继续去访问当前栈顶（前面左子节点弹出去了，现在就是栈顶）的右子节点
        if len(stack) != 0 and stack[-1].left == root:
            root = stack[-1].right
        else:
            # 没有右子树或右子树遍历完毕，强迫退栈,不然的话会一直输出右子树的值，死循环
            root = None
    return array

层序遍历——队列

# 层序遍历（宽度优先遍历BFS）
# 思想：利用队列，依次将根，左子树，右子树存入队列，按照队列的先进先出规则来实现层次遍历。
def BFS(root):
    if root == None:
        return
    queue = [root]  # 创建queue队列，保存节点
    array = []  # 保存节点值，作为结果
    while queue:
        q = queue.pop(0)  # 拿出队首节点
        array.append(q.val)  # 注意是值！
        if q.left:  # 若左节点存在
            queue.append(q.left)  # 放进队列
        if q.right:  # 若右节点存在
            queue.append(q.right)  # 放进队列
    return array

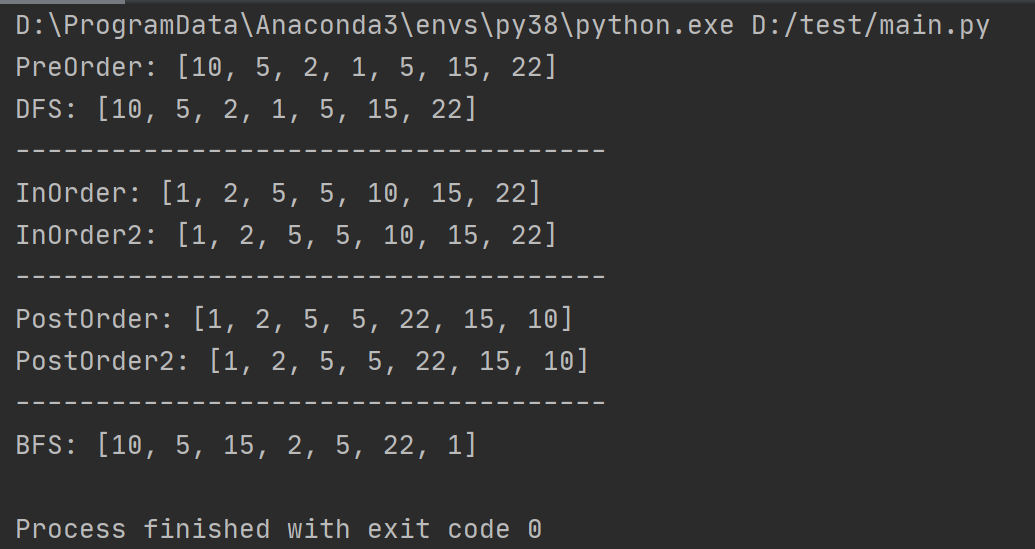
代码测试

root = TreeNode(10)
root.left = TreeNode(5)
root.right = TreeNode(15)
root.left.left = TreeNode(2)
root.left.right = TreeNode(5)
root.left.left.left = TreeNode(1)
root.right.right = TreeNode(22)

print("PreOrder:", PreOrder(root))
print("DFS:", DFS(root))
print("-------------------------------------")
print("InOrder:", InOrder(root))
print("InOrder2:", InOrder2(root))
print("-------------------------------------")
print("PostOrder:", PostOrder(root))
print("PostOrder2:", PostOrder2(root))
print("-------------------------------------")
print("BFS:", BFS(root))

☆层序遍历，牛客or力扣的输出不同

输入：{1,2,3,4,#,#,5}
返回值：[[1],[2,3],[4,5]]

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def levelOrder(self , root ):
        # write code here
        #先进先出
        if root is None:
            return
        queue=[root]
        array=[]
        while queue:
            array.append([node.val for node in queue])#不要忘了加括号！！！
            temp=[]#存储当前层的孩子节点列表
            for node in queue:
                if(node.left):
                    temp.append(node.left)
                if(node.right):
                    temp.append(node.right)
            #把queue更新成下一层的结点，继续遍历下一层
            queue=temp
        return array

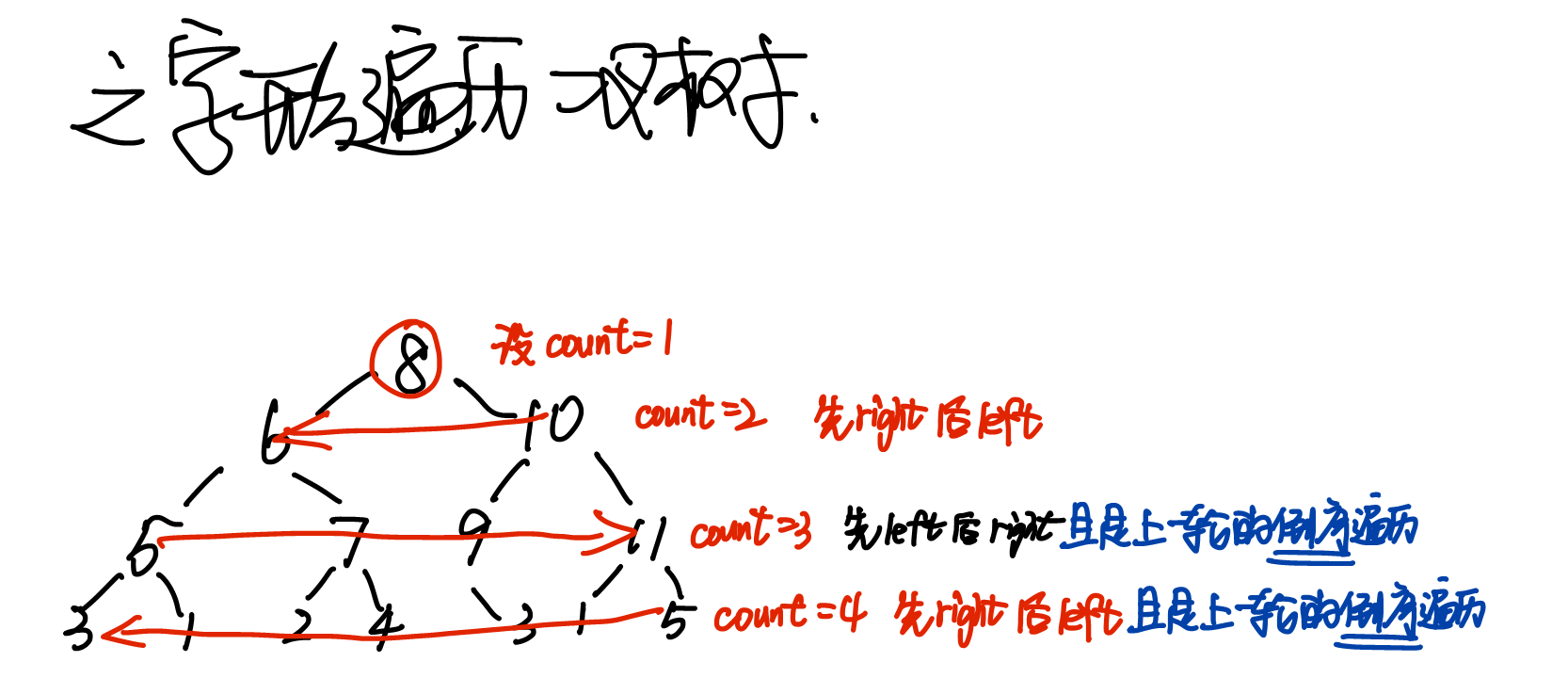
按之字形顺序打印二叉树(牛客)

给定一个二叉树，返回该二叉树的之字形层序遍历，（第一层从左向右，下一层从右向左，一直这样交替）

1 2	输入：{1,2,3,#,#,4,5} 返回值：[[1],[3,2],[4,5]]

加一个索引count判断是奇数还是偶数层，判断先左还是右，每一层都要倒序遍历上一层node

def Print(self, pRoot):
    # write code here
    if pRoot is None:
        return
    queue = [pRoot]
    result = []
    count = 1  # 判断奇偶
    while queue:
        result.append([node.val for node in queue])
        count += 1
        temp = []  # 存当前层
        if count % 2 == 1:
            for node in queue[::-1]:  # 逆序遍历queue
                if node.left:
                    temp.append(node.left)
                if node.right:
                    temp.append(node.right)
        else:
            for node in queue[::-1]:  # 逆序遍历queue
                if node.right:
                    temp.append(node.right)
                if node.left:
                    temp.append(node.left)
        queue = temp
    return result